An Exploration of the Efficacy of Gradient Descent as an Optimization Algorithm in Machine Learning and Deep Learning

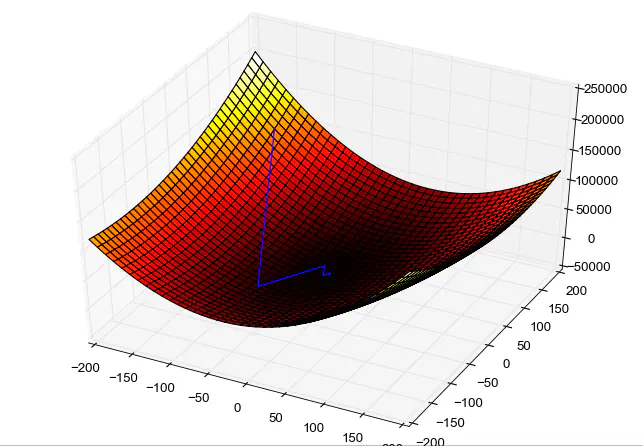7 min read Machine Learning, Deep Learning
Image credit: Wikimedia

Gradient descent is an optimization algorithm widely utilized in the fields of machine learning and deep learning for identifying the optimal parameters of a model. It involves iteratively adjusting the parameter values in the negative gradient direction of the loss function, which measures the disparity between the predicted output of the model and the actual output. The gradient represents a vector that points in the direction of the steepest ascent of the loss function. By negating this vector, the algorithm can move toward the steepest descent, approaching the loss function’s minimum.

$$ \nabla g(x, y, z) =\frac{\partial g}{\partial x}\hat{i} + \frac{\partial g}{\partial y}\hat{j} + \frac{\partial g}{\partial k}\hat{z} $$

The core idea of gradient descent is to use the gradient of the function, which gives the direction of steepest ascent, to take steps in the direction of steepest descent to find the minimum of the function.

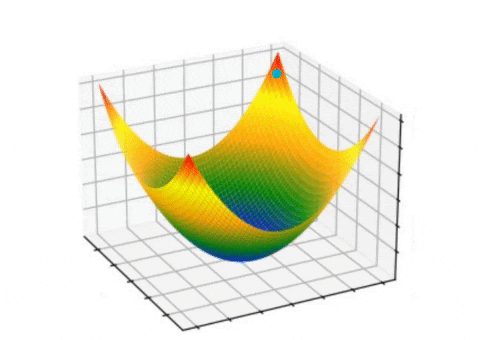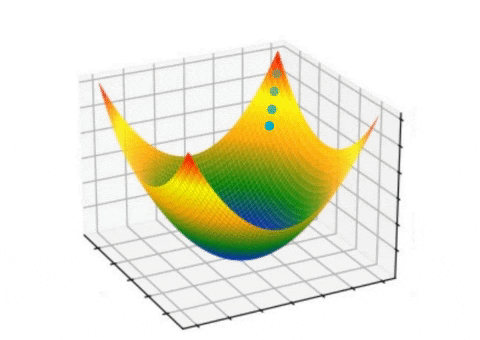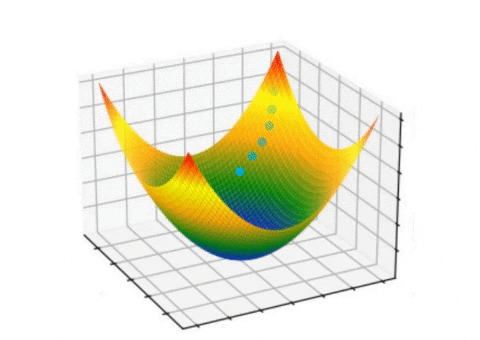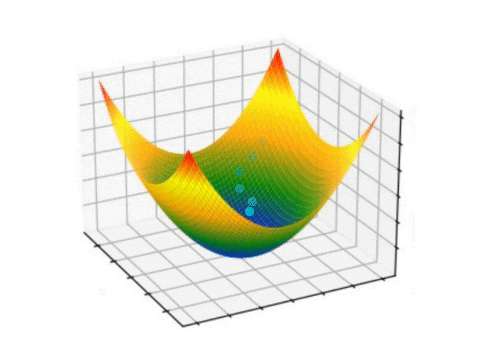
Gradient Descent
Gradient Descent

In each iteration, the algorithm calculates the gradient of the loss function with respect to the parameters and updates the parameter values. The learning rate hyperparameter controls the step size of the update, determining the magnitude of each step. Various gradient descent variants, such as batch gradient descent, stochastic gradient descent, and mini-batch gradient descent, are available depending on the dataset size and available computing resources.

Observing the process of gradient descent during the training of a two-layer neural network designed to distinguish between two classes was conducted by Matt Henderson.

The general process of gradient descent involves defining a cost function that needs to be minimized, initializing the parameters of the function, and then calculating the gradient of the cost function with respect to the parameters. This gradient is a vector that points in the direction of steepest ascent of the cost function. The algorithm then takes a step in the direction of the negative gradient, which is the direction of steepest descent, to update the parameters.

Batch Gradient Descent

Batch gradient descent is an optimization algorithm used in machine learning to minimize the cost function of a model by adjusting its parameters. In batch gradient descent, the model’s parameters are updated based on the average of the gradients of the cost function with respect to each parameter, calculated over the entire training dataset. This means that the algorithm processes the entire dataset in each iteration, making it computationally expensive for large datasets. However, batch gradient descent can converge to the optimal solution with fewer iterations compared to other optimization algorithms. Batch gradient descent is particularly useful in convex optimization problems, where the cost function has a single minimum. However, it may struggle in non-convex optimization problems, where the cost function has multiple local minima. Despite its limitations, batch gradient descent remains a popular and widely used optimization algorithm in machine learning.

Batch gradient descent calculates the gradient of the cost function with respect to all the training examples in the dataset and updates the parameters accordingly. However, this can be computationally expensive for large datasets.

Stochastic Gradient Descent (SGD)

$$ \begin{equation} \mathbf{w}^{k,p} = \mathbf{w}^{k,p-1}-\alpha_{k} \nabla h\left(\mathbf{w}^{k, p-1}, \mathbf{x}_p, y_p\right), \qquad p=1,\ldots,P \end{equation} $$

Stochastic gradient descent (SGD) is an optimization algorithm used in machine learning to minimize the cost function of a model by adjusting its parameters. Unlike batch gradient descent, which processes the entire dataset in each iteration, SGD updates the model’s parameters based on the gradient of the cost function with respect to each parameter, calculated on a randomly selected subset of the training data, called a mini-batch. This makes SGD more computationally efficient and allows it to converge faster than batch gradient descent, especially for large datasets. However, the randomness in the selection of the mini-batch can introduce noise and cause the algorithm to converge to a suboptimal solution. To mitigate this, techniques such as momentum and adaptive learning rates can be used to improve the performance of SGD. Stochastic gradient descent is widely used in machine learning and deep learning, where it forms the basis of many popular optimization algorithms such as Adam and RMSprop.

Stochastic gradient descent, on the other hand, calculates the gradient of the cost function with respect to one training example at a time and updates the parameters accordingly. This approach can be less computationally expensive, but may converge to a suboptimal minimum.

Mini-batch Gradient Descent

There are also variations of gradient descent, such as mini-batch gradient descent, which calculates the gradient of the cost function with respect to a small subset of the training examples at a time, and updates the parameters accordingly.

$$ \begin{equation} \nabla g\left(\mathbf{\mathbf{w}}\right) = \nabla \left(\underset{j=1}{\overset{J}{\sum}}\underset{p\in \Omega_j}{\sum}{h\left(\mathbf{w},\mathbf{x}_p,y_p\right)} \right)= \underset{j=1}{\overset{J}{\sum}}\nabla \left(\underset{p\in \Omega_j}{\sum}{h\left(\mathbf{w},\mathbf{x}_p,y_p\right)}\right) \end{equation} $$

Mini-batch gradient descent is a variation of the gradient descent optimization algorithm used in machine learning to minimize the cost function of a model by adjusting its parameters. Unlike batch gradient descent, which processes the entire dataset in each iteration, and stochastic gradient descent, which updates the model’s parameters based on the gradient of the cost function with respect to each parameter, calculated on a single randomly selected data point, mini-batch gradient descent updates the model’s parameters based on the gradient of the cost function with respect to each parameter, calculated on a randomly selected subset of the training data, called a mini-batch. The size of the mini-batch is typically chosen to be small enough to fit in memory, but large enough to capture enough information about the data. Mini-batch gradient descent combines the advantages of both batch gradient descent and stochastic gradient descent. It is computationally efficient, more stable, and has a faster convergence rate compared to batch gradient descent, and less noisy and less likely to get stuck in local minima compared to stochastic gradient descent. Mini-batch gradient descent is widely used in deep learning and is the most commonly used optimization algorithm for training deep neural networks.

In summary, gradient descent is a potent optimization algorithm that has become a fundamental component of numerous machine learning and deep learning applications. The choice of gradient descent variant depends on the size of the dataset and the computational resources available. Additionally, selecting an appropriate learning rate is critical for the convergence of the algorithm.

The convergence of the algorithm is typically defined as the point at which the cost function no longer decreases significantly. However, the algorithm can be sensitive to the choice of learning rate, and if it is too large, it may converge to a suboptimal minimum. Therefore, it is essential to choose an appropriate learning rate and monitor the convergence of the algorithm to ensure that it is converging to a reasonable minimum.

References:

Academic
Agung Pambudi
Agung Pambudi
Data Science | T-Shaped | Lifelong Learner | Sightseer

My research interests include Data Science, Data Mining, Machine Learning and Deep Learning.